Difference between revisions of "Path Library Improvement Project"
m |
|||
| Line 18: | Line 18: | ||
==== Breaking Cubic Beziers ==== | ==== Breaking Cubic Beziers ==== | ||
[[File:Bezier-splitting.png|thumb]] | [[File:Bezier-splitting.png|thumb]] | ||
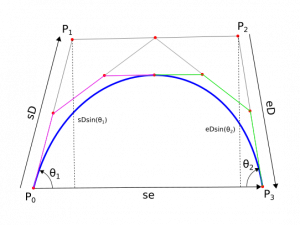
The algorithm that livarot uses to decide how/if to split a cubic curve is slightly complex to understand. Therefore, I decided it would be best to explain it with the help of a picture. The cubic bezier shown in the picture is defined by two endpoints $\vec{P_{0}}$ and $\vec{P_{3}}$ and two control points $\vec{P_{1}}$ and $\vec{P_{1}}$. | |||
Revision as of 11:30, 14 June 2020
This wiki page will hold all extra documentation that I intend to write as I progress in the project.
The first functionality that I have succeeded to implement is Path Simplification.
Path Simplification
It is a two step process:
- Given a threshold value, break a path into line segments (we call this a polyline)
- Fit cubic bezier patches on the polyline such that the total error is controlled and the number of patches are kept minimum.
Breaking up into line segments
While this process can be very simple if we simply use lib2geom's Geom::Curve abstraction with a recursive path splitting algorithm. I think it's still better to use separate pieces of codes to deal with each type of curve separately. There are two advantages to doing this. Firstly, if you know the curve type, you can use a faster algorithm to do the splitting, secondly we can use the same path splitting algorithms as livarot does and have identical results.
At the moment, I have custom code to deal with Cubic Bezier curves and Line Segments (PathFlattener::breakLine and PathFlattener::breakCubic) and for every other type a generalized function PathFlattener::breakCurve is used.
Breaking Line Segments
Usually line segments aren't further broken at all. So only their endpoint is added to the sequence. However, if the flag convertEvenLines is set, we break the line into smaller line segments such that each line segment has a length that's smaller than or equal to the threshold. This is useful in Path Simplification.
Breaking Cubic Beziers
The algorithm that livarot uses to decide how/if to split a cubic curve is slightly complex to understand. Therefore, I decided it would be best to explain it with the help of a picture. The cubic bezier shown in the picture is defined by two endpoints $\vec{P_{0}}$ and $\vec{P_{3}}$ and two control points $\vec{P_{1}}$ and $\vec{P_{1}}$.