LPE: Ellipse from Points

This page describes inkscape's Live Path Effects "Ellipse from Points" introduced in inkscape 0.93.

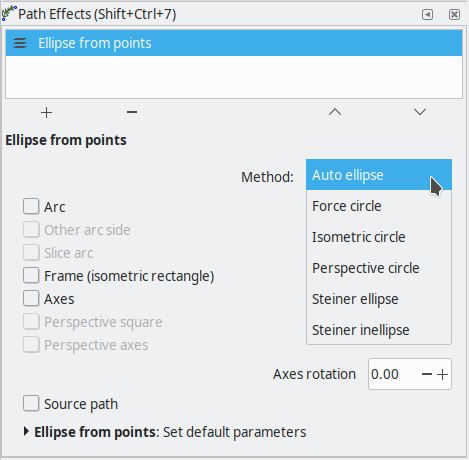
GUI Parameters

1. Method: select from
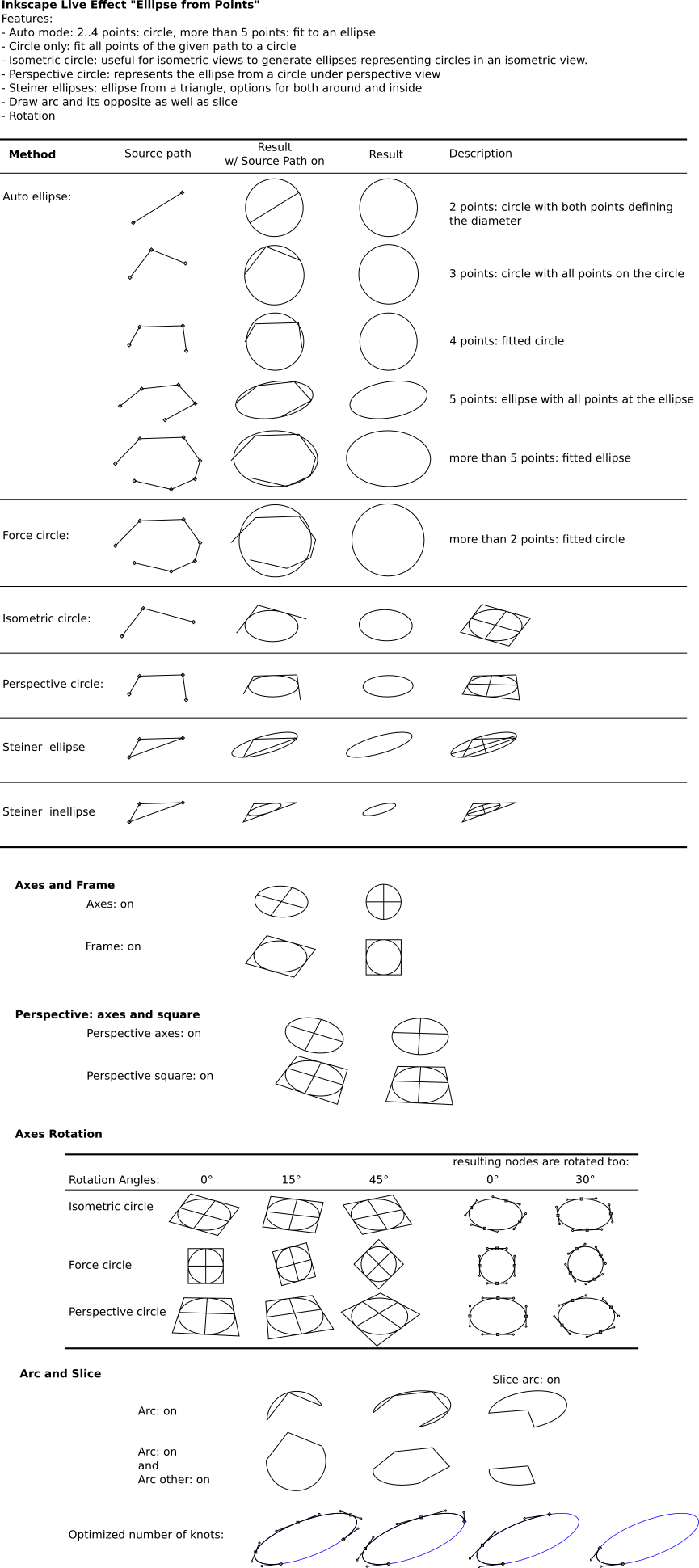
   1. Auto ellipse: if the path contains 2...4 nodes, a circle is created; if the path contains more than 5 nodes, an ellipse is created. Note, that a circle is properly defined with either 2 or 3 points and an ellipse requires at least 5 points.
   2. Force circle: similar to Auto Ellipse, but now a circle is always fitted. Requires a path with at least 2 nodes.
   3. Isometric circle: uses the first 2 edges to construct an isometric ellipse.
2. Arc: if checked, generates an (open) elliptic arc between the first and last node. Note, that for the fitting of the ellipse only the nodes of the input path count and not the order nor the form. So, going "backwards" is allowed. Just play by moving the nodes of the input path!
3. Other Arc side: if checked, uses the opposite side for the arc (only has an effect when Arc is selected).
4. Slice Arc: if checked, generates a sliced arc (only has an effect when Arc is selected).
5. Frame (isometric rectangle): if checked, generates an isometric rectangle  – a frame  – around the ellipse.
6. Axes: if checked, generates the (main) axes of the ellipse.
7. Axes rotation: rotates the whole ellipse including the resulting nodes, frame and axes (unit: [deg]).
8. Source Path: if checked, generates the source path. This is useful for modifying the source path and hence the resulting ellipse.

Examples

Example svg file for inkscape

Example saved as pdf file