Difference between revisions of "SpecFilletChamfer"
Romain2Boss (talk | contribs) m (Add category Proposals) |
|||
| Line 51: | Line 51: | ||
* A: 2geom's filet-minion toy demonstrates how to implement this to compute 'Y'. A nice emergent property of using self-intersections on the offset curves is that you can remove all tight spots, not just those on control handles. However, the results aren't very visually pleasing to me. There are no obvious numerical problems, but some difficulty in detecting loops. If a student were to take on this project we could discuss techniques for accurately detecting the bad cases. | * A: 2geom's filet-minion toy demonstrates how to implement this to compute 'Y'. A nice emergent property of using self-intersections on the offset curves is that you can remove all tight spots, not just those on control handles. However, the results aren't very visually pleasing to me. There are no obvious numerical problems, but some difficulty in detecting loops. If a student were to take on this project we could discuss techniques for accurately detecting the bad cases. | ||
[[Category:Proposals]] | |||
Latest revision as of 10:16, 31 March 2012
Launchpad Entry: https://blueprints.launchpad.net/inkscape/+spec/fillet-tool
Summary
The filleting tool will allow the user to replace the cusp of a corner on a path, with a rounding arc of specified radius. This is rather simple to the way we can round off the corners rectangles, but for arbitrary geometry.
Note that this proposed tool will only work on corners in individual paths - not on the intersections of the strokes of separate objects.
Release Note
Rationale
A fillet/chamfer tool is useful for technical drawings where fillets and chamfers are needed often, and smoothing corners in artwork.
Design
User Interface
In terms of implementation, the filleting tool must be implemented as a sub-feature within the node edit tool. With the node tool selected, the user will select a series of points in a path that they would like to fillet. The user will then click the fillet button in the node context toolbar.
With this fillet-tool-button clicked, and the an interactive fillet mode is activated. The node edit context toolbar will change to a fillet context toolbar. The fillet-tool-button will remain present on this new toolbar, but will be shown depressed to indicate that the filleting mode is activated. An edit box with spinner will be placed in the bar so that the user can choose the radius numerically. At the same time handles will be shown on the canvas to allow the user to edit the radius interactively. Helper circles will give a preview of the end result.
Once the user is happy with the fillet, the result can be committed by selecting a different tool or clicking the fillet-tool-button on toolbar (so as to un-depress it). To cancel, the user can press Esc, or can apply the change then Undo.
It might be helpful to give the choice between placing a full circle object into the corner, a tangential arc object of the fillet, or actually filleting the corner with an arc which will modify the parent path to replace the cusp.
This tool will give the option to chamfer the corner - where instead smoothing the corner with an arc, the corner is smoothed with a straight line - simply snipping the tip off.
Back End
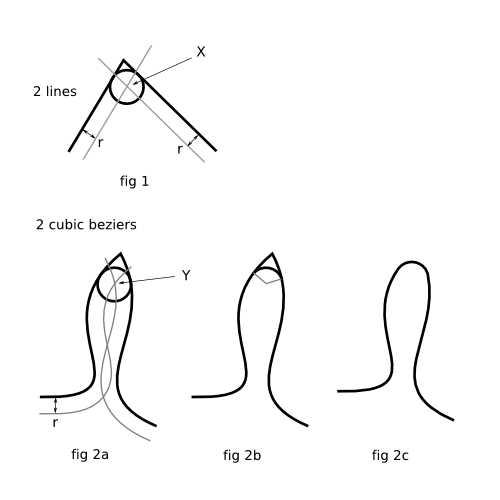
The illustration below shows the steps involved in filleting the corner of a path:
Filleting a corner is a 3-step process. First, the centre point for the arc must be calculated (X and Y in fig 1 and fig 2a). Second, the arc's sweep must be calculated so that it merges with the parent path at the tagents (fig 2b). Third, the point of the corner must be snipped off, and the arc welded on (fig 2c).
All shapes must be converted to paths before filleting can occur.
Finding point X is mathematically trivial. Finding Y is very much harder, and will require a numerical solution to a set of simultaneous equations. Note that there could potentially be more than one possible solution (as shown in fig 2a), so the closest solution to the cusp along the the length of bezier should be selected.
More ideas
See [1]
Cale Gibbard proposed another technique here, with an excellent diagram to explain it. I think it's a very good solution, relatively easy to code and more "stable" under deformations of the original curve (in particular, there is always one and only one solution...). The output arc is not a perfect circle however, and it's radius is not explicitly controlled (depends on tangent angle at the corner). Maybe both option should be tested/implemented. --jfb 22:35, 17 March 2008 (UTC)
TODO
Discussion
Existing Code?
- Q: Does anyone know of any existing code in the codebase that makes these sorts of calculations? So as to avoid reinventing the wheel and duplicating code?
- A: These kind of calculations is being widely used in CAD applications, eg. in Qcad (see: http://www.ribbonsoft.com/qcad.html ).
- A: 2geom's filet-minion toy demonstrates how to implement this to compute 'Y'. A nice emergent property of using self-intersections on the offset curves is that you can remove all tight spots, not just those on control handles. However, the results aren't very visually pleasing to me. There are no obvious numerical problems, but some difficulty in detecting loops. If a student were to take on this project we could discuss techniques for accurately detecting the bad cases.